nLab Delta-generated topological space
Context
Topology
topology (point-set topology, point-free topology)
see also differential topology, algebraic topology, functional analysis and topological homotopy theory
Basic concepts
-
fiber space, space attachment
Extra stuff, structure, properties
-
Kolmogorov space, Hausdorff space, regular space, normal space
-
sequentially compact, countably compact, locally compact, sigma-compact, paracompact, countably paracompact, strongly compact
Examples
Basic statements
-
closed subspaces of compact Hausdorff spaces are equivalently compact subspaces
-
open subspaces of compact Hausdorff spaces are locally compact
-
compact spaces equivalently have converging subnet of every net
-
continuous metric space valued function on compact metric space is uniformly continuous
-
paracompact Hausdorff spaces equivalently admit subordinate partitions of unity
-
injective proper maps to locally compact spaces are equivalently the closed embeddings
-
locally compact and second-countable spaces are sigma-compact
Theorems
Analysis Theorems
Contents
Definition
Definition
(-Generated spaces)
A -generated space (alias numerically generated space) (Smith, Dugger 03) is a topological space whose topology is the final topology induced by all continuous functions of the form , hence those whose domain is one of the standard topological simplices, for .
A morphism between -generated spaces is just a continuous function, hence the category of -generated spaces is the full subcategory on these spaces inside all TopologicalSpaces,
Remark
(as colimits of topological simplices)
Equivalently, the class of -generated spaces is the closure of the set of topological simplices under small colimits in topological spaces (see at Top – universal constructions).
Remark
(as Euclidean-generated spaces)
For each the topological simplex is a retract of the ambient Euclidean space/Cartesian space (as a non-empty convex subset of a Euclidean space it is in fact an absolute retract). Hence the identity function on factors as
and it follows that every continuous function with domain the topological simplex extends as a continuous function to Euclidean space:
Therefore the condition that a topological space be -generated (Def. ) is equivalent to saying that its topology is final with respect to all continuous functions out of Euclidean/Cartesian spaces.
Remark
(as D-topological spaces)
By Prop. below, the Euclidean-generated spaces and hence, by Remark , the -generated spaces, are equivalently those that arise from equipping a diffeological space with its D-topology, hence are, in this precise sense, the D-topological spaces. Luckily, “D-topological space” may also serve as an abbreviation for “Delta-generated topological space”.
Properties
Coreflection into all topological spaces
Proposition
(adjunction between topological spaces and diffeological spaces)
There is a pair of adjoint functors
between the categories of TopologicalSpaces and of DiffeologicalSpaces, where
-
takes a topological space to the continuous diffeology, namely the diffeological space on the same underlying set whose plots are the continuous functions (from the underlying topological space of the domain ).
-
takes a diffeological space to the diffeological topology (D-topology), namely the topological space with the same underlying set and with the final topology that makes all its plots into continuous functions: called the D-topology.
Hence a subset is an open subset in the D-topology precisely if for each plot the preimage is an open subset in the Cartesian space .
Moreover:
-
the fixed points of this adjunction TopologicalSpaces (those for which the counit is an isomorphism, hence here: a homeomorphism) are precisely the Delta-generated topological spaces (i.e. D-topological spaces):
-
this is an idempotent adjunction, which exhibits -generated/D-topological spaces as a reflective subcategory inside diffeological spaces and a coreflective subcategory inside all topological spaces:
Finally, these adjunctions are a sequence of Quillen equivalences with respect to the:
| classical model structure on topological spaces | model structure on D-topological spaces | model structure on diffeological spaces |
Caution: There was a gap in the original proof that . The gap is claimed to be filled now, see the commented references here.
Essentially these adjunctions and their properties are observed in Shimakawa, Yoshida & Haraguchi 2010, Prop. 3.1, Prop. 3.2, Lem. 3.3, see also Christensen, Sinnamon & Wu 2014, Sec. 3.2. The model structures and Quillen equivalences are due to Haraguchi 13, Thm. 3.3 (on the left) and Haraguchi-Shimakawa 13, Sec. 7 (on the right).
Proof
We spell out the existence of the idempotent adjunction (2):
First, to see we have an adjunction , we check the hom-isomorphism (here).
Let and . Write for the underlying sets. Then a morphism, hence a continuous function of the form
is a function of the underlying sets such that for every open subset and every smooth function of the form the preimage is open. But this means equivalently that for every such , is continuous. This, in turn, means equivalently that the same underlying function constitutes a smooth function .
In summary, we thus have a bijection of hom-sets
given simply as the identity on the underlying functions of underlying sets. This makes it immediate that this hom-isomorphism is natural in and and this establishes the adjunction.
Next, to see that the D-topological spaces are the fixed points of this adjunction, we apply the above natural bijection on hom-sets to the case
to find that the counit of the adjunction
is given by the identity function on the underlying sets .
Therefore is an isomorphism, namely a homeomorphism, precisely if the open subsets of with respect to the topology on are precisely those with respect to the topology on , which means equivalently that the open subsets of coincide with those whose pre-images under all continuous functions are open. This means equivalently that is a D-topological space.
Finally, to see that we have an idempotent adjunction, it is sufficient to check (by this Prop.) that the comonad
is an idempotent comonad, hence that
is a natural isomorphism. But, as before for the adjunction counit , we have that also the adjunction unit is the identity function on the underlying sets. Therefore, this being a natural isomorphism is equivalent to the operation of passing to the D-topological refinement of the topology of a topological space being an idempotent operation, which is clearly the case.
Topological homotopy type and diffeological shape
Definition
(diffeological singular simplicial set)
Consider the simplicial diffeological space
which in degree is the standard extended n-simplex inside Cartesian space , equipped with its sub-diffeology.
This induces a nerve and realization adjunction between diffeological spaces and simplicial sets:
where the right adjoint is the diffeological singular simplicial set functor .
(e.g. Christensen-Wu 13, Def. 4.3)
Remark
(diffeological singular simplicial set as path ∞-groupoid)
Regarding simplicial sets as presenting ∞-groupoids, we may think of (Def. ) as the path ∞-groupoid of the diffeological space .
In fact, by the discussion at shape via cohesive path ∞-groupoid we have that is equvialent to the shape of diffeological spaces regarded as objects of the cohesive (∞,1)-topos of smooth ∞-groupoids:
Proposition
(topological homotopy type is cohesive shape of continuous diffeology)
For every TopologicalSpaces, the cohesive shape/path ∞-groupoid presented by its diffeological singular simplicial set (Def. , Remark ) of its continuous diffeology is naturallyweak homotopy equivalent to the homotopy type of presented by the ordinary singular simplicial set:
Model category structure
Proposition
(model structure on Delta-generated topological spaces)
The category of -generated spaces carries the structure of a cofibrantly generated model category with the same generating (acyclic) cofibrations as for the classical model structure on topological spaces and such that the coreflection into all TopologicalSpaces (Prop. ) is a Quillen equivalence to the classical model structure on topological spaces.
This Quillen equivalence factors through the model structure on compactly generated topological spaces (e.g. Gaucher 2007, p. 7):
As a convenient category of topological spaces
Proposition
The category of Euclidean-generated spaces/-generated spaces (Def. ) is a Cartesian closed category.
Explicitly, the internal hom is, equivalently:
-
the image under (1) of the mapping space with the compact-open topology:
-
the image under (1) of the internal hom formed in diffeological spaces:
In fact, SYH 10, Prop. 4.7 state something stronger, topologically characterizing even before applying to it. This stronger statement has a nice form when specialized to CW-complexes:
Proposition
The category of Euclidean-generated spaces/-generated spaces (Def. ) contains all CW-complexes.
Proposition
(diffeological internal hom out of CW-complexes)
If is a CW-complex, regarded as an object in via Prop. , then for every their internal hom formed in diffeological spaces is isomorphic to the image under (1) of the mapping space with its compact open topology:
Proof
This is the following combination of statements from SYH 10:
-
Prop. 4.7 there says that, in general:
(where “” is defined on their p. 6),
-
Prop. 4.3 there implies that, when is a CW-complex, as assumed here:
In summary:
Proposition
(Euclidean-generated spaces are convenient)
The category of Euclidean-generated spaces/-generated spaces (Def. ) is a convenient category of topological spaces in that:
-
it is coreflective in TopSp (by Prop. )
-
it is complete and cocomplete category
(by Vogt 1971; SYH 10, Prop. 3.4)
-
it is locally presentable (FR 08, Cor. 3.7),
-
it contains all CW-complexes (Prop. ),
-
it is cartesian closed, with internal hom expressible as in Prop. .
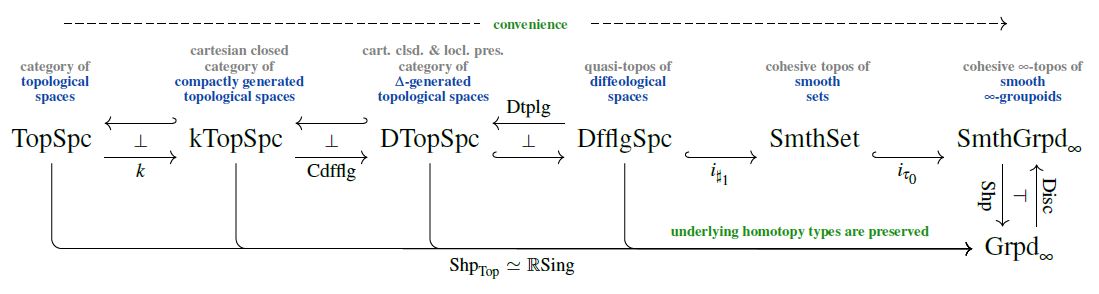
Moreover, in further summary of the discussion further above, this convenient category of topological spaces is:
-
a full subcategory of the quasi-topos of diffeological spaces (see there),
-
which is in turn a full subcategory of the cohesive topos of smooth sets (see there);
-
which in turn is a full sub--category of the cohesive -topos of smooth -groupoids
such that the canonical shape modality (the smooth path ∞-groupoid construction) still sees the correct underlying homotopy type of topological spaces (SS20, Ex. 3.18, see also at model structure on Delta-generated topological spaces):
Examples
Example
Given a smooth manifold — hence a topological space equipped with a smooth structure — canonically regarded as a diffeological space, then its D-topology (2) coincides with its ordinary topology:
Remark
Together with the adjunction of Prop. , Ex. implies that for a smooth manifold and a general topological space, there is a natural bijection between
-
morphisms of diffeological spaces,
because
Related concepts
References
General
-generated spaces were originally proposed by Jeff Smith as a nice category of spaces for homotopy theory.
-
Jeff Smith, A really convenient category of topological spaces (unpublished and possibly non-existent, according to Dugger 03, p. 4)
-
Daniel Dugger, Notes on Delta-generated spaces, 2003 (web, pdf)
A proof that the category of -generated spaces is locally presentable is in:
- Lisbeth Fajstrup, Jiří Rosický, Thm. 3.6 of: A convenient category for directed homotopy, Theory and Applications of Categories, Vol. 21, 2008, No. 1, pp 7-20. (arXiv:0708.3937, tac:21-01)
See also at directed homotopy theory.
The model structure on Delta-generated topological spaces Quillen equivalent to the classical model structure on topological spaces is due to
- Tadayuki Haraguchi, On model structure for coreflective subcategories of a model category, Math. J. Okayama Univ.57(2015), 79–84 (arXiv:1304.3622, MR3289294, Zbl 1311.55027)
Discussion in the generality of subcategory-generated spaces, including compactly generated topological spaces:
- Philippe Gaucher, Section 2 of: Homotopical interpretation of globular complex by multipointed d-space, Theory and Applications of Categories, vol. 22, number 22, 588-621, 2009 (arXiv:0710.3553)
along the lines of
-
Rainer M. Vogt, Convenient categories of topological spaces for homotopy theory, Arch. Math 22, 545–555 (1971) (doi:10.1007/BF01222616)
-
Martín Escardó, Jimmie Lawson, Alex Simpson, Section 3 of: Comparing Cartesian closed categories of (core) compactly generated spaces, Topology and its Applications Volume 143, Issues 1–3, 28 August 2004, Pages 105-145 (doi:10.1016/j.topol.2004.02.011)
Discussion about the q-model structure, the m-model structure, the h-model structure and the notion of -Hausdorff -generated space (a natural separation condition for -generated spaces) in:
- Philippe Gaucher, Section 2 and Appendix B of: Left properness of flows, Theory and Applications of Categories, 37 19 (2021) 562-612 (arXiv:1907.01454, TAC:37-19)
Relation to diffeological spaces
Relation to diffeological spaces:
-
Kazuhisa Shimakawa, K. Yoshida, Tadayuki Haraguchi, Homology and cohomology via enriched bifunctors, Kyushu Journal of Mathematics, 2018 Volume 72 Issue 2 Pages 239-252 (arXiv:1010.3336, doi:10.2206/kyushujm.72.239)
-
J. Daniel Christensen, Gord Sinnamon, Enxin Wu, Sec. 3.2 of: The -topology for diffeological spaces, Pacific Journal of Mathematics 272 1 (2014) 87-110 [arXiv:1302.2935, doi:10.2140/pjm.2014.272.87]
Last revised on June 22, 2025 at 21:48:44. See the history of this page for a list of all contributions to it.